概念
-
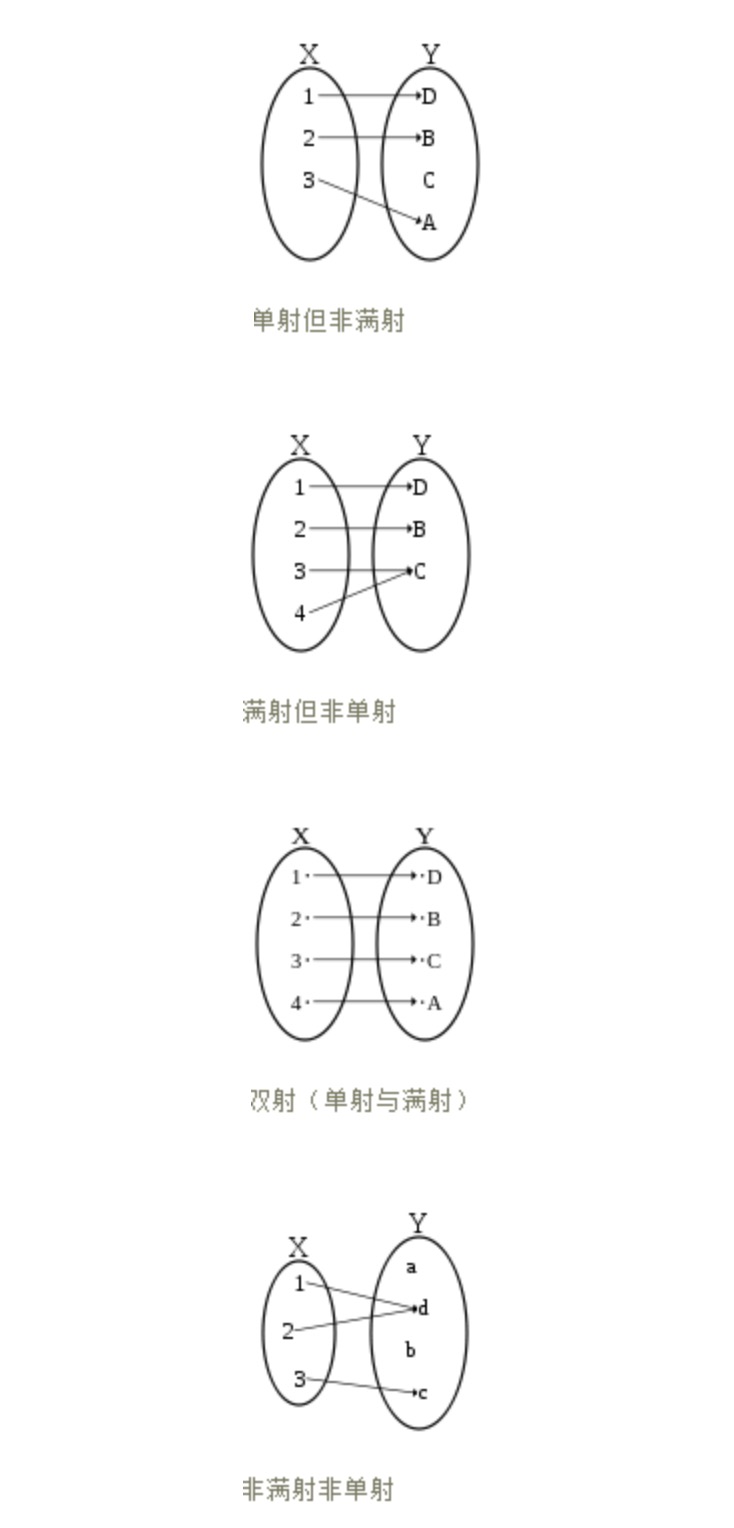
单射(injection):每一个x都有唯一的y与之对应;
-
满射(surjection):每一个y都必有至少一个x与之对应;
-
双射(又叫一一对应,bijection):每一个x都有y与之对应,每一个y都有x与之对应。
例子
今天,把x比作萝卜,y比作坑:
-
单射就是一个萝卜一个坑,有的坑有可能没萝卜;
-
满射就是所有坑都有萝卜,有的坑可能有不止一个萝卜;
-
双射就是严格的一个萝卜一个坑,一个坑一个萝卜,所有萝卜都有坑,所有坑都有萝卜。
符号化表示
injection:
$$\displaystyle \forall a,b\in X,;;f(a)=f(b)\Rightarrow a=b$$
surjection:
$$\forall y\in Y,,\exists x\in X,;;f(x)=y$$
bijection:
$$\displaystyle \forall y\in Y,\exists !x\in X{\text}y=f(x)$$
where $\displaystyle \exists !x$ means there exists exactly one x.
For all functions, the following holds:
$$\displaystyle \forall x\in X,\exists !y\in Y{\text}y=f(x).$$
